How to Draw a Cumulative Frequency Curve TUTORIAL

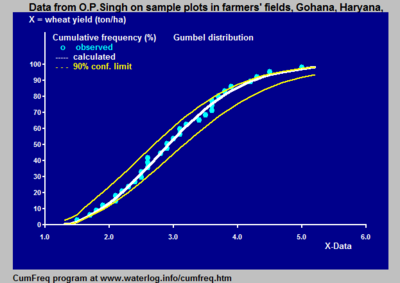
Cumulative frequency distribution, adapted cumulative probability distribution, and confidence intervals

Cumulative frequency assay is the analysis of the frequency of occurrence of values of a phenomenon less than a reference value. The miracle may exist time- or space-dependent. Cumulative frequency is also called frequency of non-exceedance.

Cumulative frequency analysis is performed to obtain insight into how oft a certain phenomenon (feature) is below a sure value. This may help in describing or explaining a situation in which the phenomenon is involved, or in planning interventions, for case in overflowing protection.^[1]

This statistical technique can exist used to see how likely an event like a overflowing is going to happen over again in the future, based on how ofttimes information technology happened in the past. It tin be adapted to bring in things like climate change causing wetter winters and drier summers.

Principles [edit]

Definitions [edit]

Frequency analysis^[2] is the assay of how often, or how frequently, an observed phenomenon occurs in a certain range.

Frequency assay applies to a record of length North of observed data X ₁, 10 _ii, X ₃ . . . 10 _{Due north} on a variable phenomenon X. The record may be time-dependent (e.g. rainfall measured in one spot) or infinite-dependent (east.1000. crop yields in an area) or otherwise.

The cumulative frequency M _Xr of a reference value Xr is the frequency by which the observed values X are less than or equal to Xr.

The relative cumulative frequency Fc can be calculated from:

Fc = M _Xr / Northward

where Northward is the number of information

Briefly this expression tin be noted as:

Fc = M / N

When Xr = Xmin, where Xmin is the unique minimum value observed, information technology is institute that Fc = one/North, considering Chiliad = ane. On the other hand, when Xr=Xmax, where Xmax is the unique maximum value observed, it is plant that Fc = one, because M = N. Hence, when Fc = 1 this signifies that Xr is a value whereby all data are less than or equal to Xr.

In percentage the equation reads:

Fc (%) = 100 M / N

Probability approximate [edit]

From cumulative frequency [edit]

The cumulative probability Pc of X to be smaller than or equal to Xr can be estimated in several ways on the basis of the cumulative frequency M .

One manner is to utilize the relative cumulative frequency Fc as an estimate.

Another mode is to take into account the possibility that in rare cases Ten may assume values larger than the observed maximum Xmax. This can be done dividing the cumulative frequency M by Northward+1 instead of N. The estimate so becomes:

Pc = Thousand / (Northward+1)

There exist as well other proposals for the denominator (encounter plotting positions).

By ranking technique [edit]

Ranked cumulative probabilities

The estimation of probability is made easier by ranking the data.

When the observed data of X are arranged in ascending order (10 ₁ ≤ Ten ₂ ≤ Ten ₃ ≤ . . . ≤ X _N , the minimum first and the maximum last), and Ri is the rank number of the observation Xi, where the adfix i indicates the serial number in the range of ascending data, so the cumulative probability may be estimated by:

Pc = Ri / (Northward + 1)

When, on the other hand, the observed data from X are arranged in descending order, the maximum first and the minimum concluding, and Rj is the rank number of the observation Xj, the cumulative probability may exist estimated by:

Pc = 1 − Rj / (N + 1)

Fitting of probability distributions [edit]

Continuous distributions [edit]

Different cumulative normal probability distributions with their parameters

To present the cumulative frequency distribution as a continuous mathematical equation instead of a discrete set of data, 1 may endeavor to fit the cumulative frequency distribution to a known cumulative probability distribution,.^{[2] [3]}
If successful, the known equation is enough to report the frequency distribution and a tabular array of data will not be required. Further, the equation helps interpolation and extrapolation. Nonetheless, intendance should be taken with extrapolating a cumulative frequency distribution, because this may exist a source of errors. One possible error is that the frequency distribution does not follow the selected probability distribution whatsoever more than across the range of the observed information.

Any equation that gives the value 1 when integrated from a lower limit to an upper limit like-minded well with the data range, can exist used as a probability distribution for plumbing fixtures. A sample of probability distributions that may exist used can be found in probability distributions.

Probability distributions can be fitted by several methods,^[two] for example:

• the parametric method, determining the parameters like hateful and standard deviation from the 10 information using the method of moments, the maximum likelihood method and the method of probability weighted moments.
• the regression method, linearizing the probability distribution through transformation and determining the parameters from a linear regression of the transformed Pc (obtained from ranking) on the transformed X data.

Application of both types of methods using for case

• the normal distribution, the lognormal distribution, the logistic distribution, the loglogistic distribution, the exponential distribution, the Fréchet distribution, the Gumbel distribution, the Pareto distribution, the Weibull distribution and other

oft shows that a number of distributions fit the data well and do not yield significantly different results, while the differences between them may be small compared to the width of the confidence interval.^[2] This illustrates that it may be difficult to decide which distribution gives amend results. For instance, approximately normally distributed data sets can exist fitted to a big number of unlike probability distributions.^[4] while negatively skewed distributions tin can be fitted to square normal and mirrored Gumbel distributions.^[5]

Cumulative frequency distribution with a discontinuity

Discontinuous distributions [edit]

Sometimes it is possible to fit one type of probability distribution to the lower part of the data range and another blazon to the higher part, separated by a breakpoint, whereby the overall fit is improved.

The figure gives an example of a useful introduction of such a discontinuous distribution for rainfall information in northern Peru, where the climate is subject field to the beliefs Pacific Ocean current El Niño. When the Niño extends to the s of Ecuador and enters the bounding main forth the coast of Republic of peru, the climate in Northern Peru becomes tropical and moisture. When the Niño does not accomplish Peru, the climate is semi-arid. For this reason, the higher rainfalls follow a unlike frequency distribution than the lower rainfalls.^[6]

Prediction [edit]

Dubiety [edit]

When a cumulative frequency distribution is derived from a record of data, it can be questioned if it tin can be used for predictions.^[7] For example, given a distribution of river discharges for the years 1950–2000, can this distribution be used to predict how often a certain river discharge will be exceeded in the years 2000–50? The answer is yes, provided that the ecology atmospheric condition practice not modify. If the environmental weather do change, such as alterations in the infrastructure of the river's watershed or in the rainfall pattern due to climatic changes, the prediction on the ground of the historical record is subject to a systematic error. Even when there is no systematic error, there may exist a random mistake, because past take chances the observed discharges during 1950 − 2000 may have been higher or lower than normal, while on the other hand the discharges from 2000 to 2050 may past adventure be lower or higher than normal. Problems around this take been explored in the book The Black Swan.

Confidence intervals [edit]

Binomial distributions for Pc = 0.1 (blue), 0.5 (greenish) and 0.8 (crimson) in a sample of size Northward = xx. The distribution is symmetrical only when Pc = 0.5

90% binomial confidence belts on a log calibration.

Probability theory can help to estimate the range in which the random error may be. In the case of cumulative frequency at that place are only 2 possibilities: a certain reference value 10 is exceeded or information technology is non exceeded. The sum of frequency of exceedance and cumulative frequency is one or 100%. Therefore, the binomial distribution can be used in estimating the range of the random error.

According to the normal theory, the binomial distribution tin be approximated and for large N standard deviation Sd can be calculated as follows:

• Sd =√ Pc(i − Pc)/Northward

where Pc is the cumulative probability and N is the number of data. It is seen that the standard deviation Sd reduces at an increasing number of observations N.

The determination of the conviction interval of Pc makes utilise of Student's t-test (t). The value of t depends on the number of information and the confidence level of the estimate of the confidence interval. Then, the lower (50) and upper (U) confidence limits of Pc in a symmetrical distribution are found from:

• 50 =Pc −t⋅Sd
• U =Pc +t⋅Sd

This is known as Wald interval.^[8] Nonetheless, the binomial distribution is just symmetrical around the hateful when Pc = 0.5, simply it becomes asymmetrical and more and more skew when Pc approaches 0 or 1. Therefore, by approximation, Pc and ane−Pc tin exist used as weight factors in the assignation of t.Sd to L and U :

• L =Pc − ii⋅Pc⋅t⋅Sd
• U =Pc + 2⋅(1−Pc)⋅t⋅Sd

where information technology tin be seen that these expressions for Pc = 0.five are the same as the previous ones.

Example

N = 25, Pc = 0.8, Sd = 0.08, confidence level is 90%, t = 1.71, L = 0.58, U = 0.85 Thus, with 90% confidence, it is found that 0.58 < Pc < 0.85 Nevertheless, there is 10% chance that Pc < 0.58, or Pc > 0.85

Notes

• The Wald interval is known to perform poorly.^{[nine] [x] [11]}
• The Wilson score interval^[12] provides confidence interval for binomial distributions based on score tests and has better sample coverage, see^[13] and binomial proportion conviction interval for a more than detailed overview.
• Instead of the "Wilson score interval" the "Wald interval" can too exist used provided the to a higher place weight factors are included.

Render period [edit]

Render periods and confidence chugalug. The bend of the return periods increases exponentially.

The cumulative probability Pc tin can also be called probability of non-exceedance. The probability of exceedance Pe (also called survival function) is found from:

• Pe = 1 −Pc

The return period T defined every bit:

• T = ane/Pe

and indicates the expected number of observations that have to exist washed over again to find the value of the variable in study greater than the value used for T.
The upper (T_U ) and lower (T_L ) confidence limits of return periods tin exist found respectively equally:

• T_U = 1/(one−U)
• T_Fifty = 1/(1−L)

For farthermost values of the variable in study, U is close to ane and minor changes in U originate large changes in T_U . Hence, the estimated render period of extreme values is subject to a large random fault. Moreover, the confidence intervals found hold for a long-term prediction. For predictions at a shorter run, the conviction intervals U−50 and T_U −T₅₀ may actually be wider. Together with the limited certainty (less than 100%) used in the t−test, this explains why, for example, a 100-year rainfall might occur twice in ten years.

9 return-period curves of fifty-year samples from a theoretical 1000-year record (base line)

The strict notion of render period actually has a meaning only when it concerns a time-dependent phenomenon, like betoken rainfall. The render period then corresponds to the expected waiting fourth dimension until the exceedance occurs again. The return menstruation has the same dimension as the fourth dimension for which each observation is representative. For example, when the observations concern daily rainfalls, the return menstruum is expressed in days, and for yearly rainfalls information technology is in years.

Need for confidence belts [edit]

The effigy shows the variation that may occur when obtaining samples of a variate that follows a certain probability distribution. The information were provided by Benson.^[1]

The confidence belt around an experimental cumulative frequency or render period bend gives an impression of the region in which the true distribution may be found.

Also, it clarifies that the experimentally found best plumbing fixtures probability distribution may deviate from the true distribution.

Histogram [edit]

Histogram derived from the adapted cumulative probability distribution

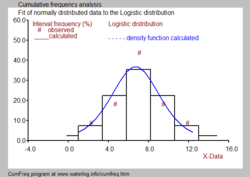
Histogram and probability density part, derived from the cumulative probability distribution, for a logistic distribution.

The observed data tin be arranged in classes or groups with serial number k. Each grouping has a lower limit (L_k ) and an upper limit (U₁₀₀₀ ). When the grade (thou) contains m_k data and the full number of data is Northward, then the relative course or group frequency is found from:

• Fg(Fifty_k < X ≤ U_k) =chiliad_grand / N

or briefly:

• Fg_g  =thou / N

or in percentage:

• Fg(%) = 100m / N

The presentation of all form frequencies gives a frequency distribution, or histogram. Histograms, even when fabricated from the aforementioned record, are different for different class limits.

The histogram can also be derived from the fitted cumulative probability distribution:

• Pg_k = Pc(U_thousand ) − Pc(L_thou )

There may exist a divergence between Fg_k and Pg_k due to the deviations of the observed data from the fitted distribution (run into blue figure).

Often it is desired to combine the histogram with a probability density office as depicted in the blackness and white moving picture.

Meet also [edit]

• Binomial proportion confidence interval
• Cumulative distribution function
• Distribution fitting
• Frequency (statistics)
• Frequency of exceedance
• cumulative quantities (logistics)

References [edit]

1. ^ ^{a b} Benson, Grand.A. 1960. Characteristics of frequency curves based on a theoretical m-year record. In: T.Dalrymple (ed.), Flood frequency analysis. U.Southward. Geological Survey Water Supply paper 1543-A, pp. 51–71
2. ^ ^{a b c d} Frequency and Regression Analysis. Chapter half-dozen in: H.P. Ritzema (ed., 1994), Drainage Principles and Applications, Publ. 16, pp. 175–224, International Institute for Land Reclamation and Improvement (ILRI), Wageningen, The Netherlands. ISBN xc-70754-33-9 . Costless download from the webpage [i] under nr. 12, or straight as PDF : [ii]
3. ^ David Vose, Fitting distributions to information
4. ^ Case of an approximately normally distributed data fix to which a big number of unlike probability distributions tin exist fitted, [iii]
5. ^ Left (negatively) skewed frequency histograms tin can be fitted to square normal or mirrored Gumbel probability functions. [four]
6. ^ CumFreq, a program for cumulative frequency analysis with confidence bands, render periods, and a discontinuity option. Gratuitous download from : [five]
7. ^ Silvia Masciocchi, 2012, Statistical Methods in Particle Physics, Lecture 11, Winter Semester 2012 / 13, GSI Darmstadt. [six]
8. ^ Wald, A.; J. Wolfowitz (1939). "Confidence limits for continuous distribution functions". The Annals of Mathematical Statistics. 10 (2): 105–118. doi:10.1214/aoms/1177732209.
9. ^ Ghosh, B.K (1979). "A comparison of some gauge confidence intervals for the binomial parameter". Journal of the American Statistical Association. 74 (368): 894–900. doi:10.1080/01621459.1979.10481051.
10. ^ Blyth, C.R.; H.A. Still (1983). "Binomial conviction intervals". Journal of the American Statistical Association. 78 (381): 108–116. doi:10.1080/01621459.1983.10477938.
11. ^ Agresti, A.; B. Caffo (2000). "Simple and effective confidence intervals for pro- portions and differences of proportions result from calculation ii successes and two failures". The American Statistician. 54 (4): 280–288. doi:10.1080/00031305.2000.10474560. S2CID 18880883.
12. ^ Wilson, E.B. (1927). "Likely inference, the law of succession, and statistical inference". Journal of the American Statistical Clan. 22 (158): 209–212. doi:10.1080/01621459.1927.10502953.
13. ^ Hogg, R.V. (2001). Probability and statistical inference (6th ed.). Prentice Hall, NJ: Upper Saddle River.

DOWNLOAD HERE

How to Draw a Cumulative Frequency Curve TUTORIAL

Posted by: lynnvould1983.blogspot.com